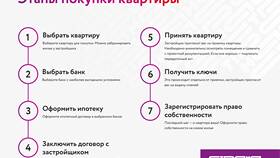
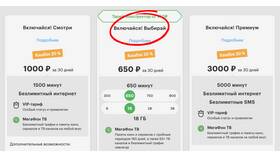
Вычисление процентов - важный математический навык, применяемый в финансах, статистике и повседневной жизни. Рассмотрим основные методы расчетов.
Содержание
Базовые понятия
Процент - сотая доля числа, обозначаемая знаком %. 1% = 1/100 = 0.01. Все вычисления основаны на этом соотношении.
Основные формулы расчета
| Тип расчета | Формула |
| Процент от числа | (Число × Процент) ÷ 100 |
| Число по проценту | (Часть × 100) ÷ Процент |
| Процентное соотношение | (Часть ÷ Целое) × 100 |
Пошаговые примеры вычислений
Нахождение процента от числа
- Задача: найти 25% от 80
- Решение: (80 × 25) ÷ 100 = 20
Нахождение числа по проценту
- Задача: 15 составляет 30% от какого числа?
- Решение: (15 × 100) ÷ 30 = 50
Нахождение процентного соотношения
- Задача: сколько процентов составляет 8 от 40?
- Решение: (8 ÷ 40) × 100 = 20%
Расчет сложных процентов
Формула сложных процентов:
Итоговая сумма = Начальная сумма × (1 + Ставка/100)периоды
| Пример | Расчет |
| 1000 руб под 10% годовых на 2 года | 1000 × (1 + 10/100)2 = 1210 руб |
Практические методы вычисления
Упрощенные расчеты
- 10% от числа = число ÷ 10
- 1% от числа = число ÷ 100
- 50% от числа = число ÷ 2
Последовательные вычисления
- Найти 1% от числа
- Умножить на нужный процент
- Пример: 17% от 200 = (200 ÷ 100) × 17 = 34
Применение в финансовых расчетах
| Сфера | Пример вычисления |
| Кредиты | Расчет ежемесячных платежей |
| Вклады | Определение доходности |
| Скидки | Вычисление суммы экономии |
| Налоги | Расчет налоговых отчислений |
Проверка правильности расчетов
Методы проверки:
- Обратный расчет (от результата к исходным данным)
- Использование альтернативного метода вычисления
- Применение калькулятора для верификации
- Оценка правдоподобности результата
Освоение методов вычисления процентов позволяет уверенно решать широкий круг практических задач в различных сферах деятельности.