В евклидовой геометрии сумма внутренних углов любого треугольника всегда равна 180 градусам. Рассмотрим несколько способов доказательства этого фундаментального свойства треугольников.
Содержание
Доказательство через параллельные прямые
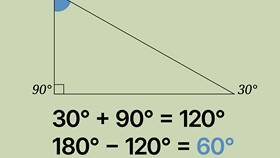
- Рассмотрим произвольный треугольник ABC
- Проведем через вершину B прямую DE, параллельную стороне AC
- Углы DBA и BAC равны как накрест лежащие при параллельных прямых DE и AC и секущей AB
- Углы EBC и BCA равны как накрест лежащие при тех же параллельных прямых и секущей BC
- Углы DBA, ABC и EBC образуют развернутый угол, равный 180°
- Следовательно, ∠BAC + ∠ABC + ∠BCA = 180°
Графическое доказательство
| Шаг | Действие |
| 1 | Нарисуйте любой треугольник и обозначьте его вершины A, B, C |
| 2 | Вырежьте треугольник из бумаги |
| 3 | Оторвите или отрежьте все три угла |
| 4 | Сложите оторванные углы вершинами вместе |
| 5 | Убедитесь, что они образуют прямую линию (180°) |
Алгебраическое доказательство
Рассмотрим доказательство через сумму углов многоугольника:
- Сумма углов n-угольника равна 180°(n-2)
- Для треугольника n=3
- Следовательно, сумма углов = 180°(3-2) = 180°
Доказательство с использованием внешнего угла
- Продолжим сторону BC треугольника ABC
- Обозначим внешний угол при вершине C как ∠ACD
- По свойству внешнего угла: ∠ACD = ∠BAC + ∠ABC
- Углы ACD и ACB смежные, их сумма равна 180°
- Подставим: ∠BAC + ∠ABC + ∠ACB = 180°
Важные замечания:
- Данное доказательство верно только для евклидовой геометрии
- В сферической геометрии сумма углов треугольника превышает 180°
- В геометрии Лобачевского сумма углов треугольника меньше 180°
Практическое применение теоремы
Знание того, что сумма углов треугольника равна 180°, позволяет:
- Находить неизвестные углы треугольника
- Доказывать другие геометрические теоремы
- Решать задачи на построение
- Проверять корректность геометрических вычислений